Page 31 - Demo

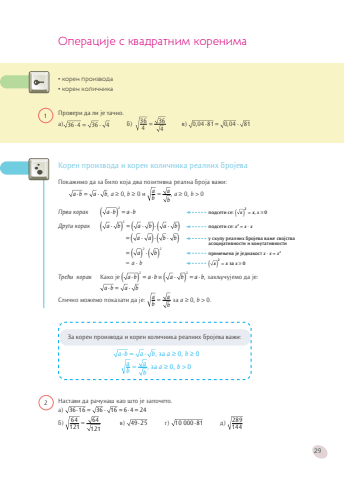
29%u041e%u043f%u0435%u0440%u0430%u0446%u0438%u0458%u0435 %u0441 %u043a%u0432%u0430%u0434%u0440%u0430%u0442%u043d%u0438%u043c %u043a%u043e%u0440%u0435%u043d%u0438%u043c%u0430Proveri da li je ta~no.a) 36%u22c5 = 4 36 4 %u22c5 b) 364364 = v) 0 0, , 4 8%u22c5 =1 0 04 %u22c5 81%u2022 %u043a%u043e%u0440%u0435%u043d %u043f%u0440%u043e%u0438%u0437%u0432%u043e%u0434%u0430%u2022 %u043a%u043e%u0440%u0435%u043d %u043a%u043e%u043b%u0438%u0447%u043d%u0438%u043a%u04301Koren proizvoda i koren koli~nika realnih brojeva Poka`imo da za bilo koja dva pozitivna realna broja va`i: a b%u22c5 = a b %u22c5 , a %u2265 0, b %u2265 0 i abab = , a %u2265 0, b > 0Prvi korak ( ) a b%u22c5 = %u22c5 a b 2 podseti se: ( ) x x =2, x %u2265 0Drugi korak ( ) a b %u22c5 = %u22c5 ( ) a b %u22c5 %u22c5 ( ) a b 2 podseti se: x2 = x %u22c5 x= %u22c5 ( ) a a %u22c5 %u22c5 ( ) b b u skupu realnih brojeva va`e svojstva asocijativnosti i komutativnosti= ( ) a b %u22c5( ) 2 2 primewena je jednakost x %u22c5 x = x2= a %u22c5 b ( ) x x =2za x %u2265 0Tre}i korak Kako je ( ) a b%u22c5 = %u22c5 a b 2 i ( ) a b %u22c5 = %u22c5 a b 2, zakqu~ujemo da je:a b%u22c5 = a b %u22c5Sli~no mo`emo pokazati da je: abab = za a %u2265 0, b > 0.Za koren proizvoda i koren koli~nika realnih brojeva va`i:a b%u22c5 = a b %u22c5 , za a %u2265 0, b %u2265 0abab = , za a %u2265 0, b > 0Nastavi da ra~una{ kao {to je zapo~eto.a) 36%u22c5 = 16 36 %u22c5 = 16 6 4%u22c5 = 24b) 6412164121 = v) 49%u22c525 g) 10 000%u22c581 d) 2891442